SINAPPSI

1. Introduzione

Le microsimulazioni sono uno strumento per l’analisi controfattuale, sia ex-ante che ex-post. L’idea sottostante ai modelli di microsimulazione è infatti quella di simulare ciò che potrebbe accadere ad una data popolazione in presenza di specifiche politiche. La simulazione avviene a livello delle unità micro – individui, famiglie o imprese – consentendo quindi un livello di dettaglio molto fine per la specificazione sia del contesto istituzionale, che dei comportamenti individuali, e la possibilità di aggregare i risultati in maniera flessibile.

I primi modelli di microsimulazione vedono la luce negli anni ’60 e ’70 del secolo scorso, quando l’avvento dei calcolatori rende praticabile la geniale intuizione di Guy Orcutt (Orcutt 1957), così come parafrasata in Klevmarken (2001):

 

“In microsimulation modelling there is no need to make assumptions about the average economic man. Although unpractical, we can in principle model every man.”

 

Martini e Trivellato (1997, p. 85) definiscono i modelli di microsimulazione come:

 

“computer programs that simulate aggregate and distributional e?ects of a policy, by implementing the provisions of the policy on a representative sample of individuals and families, and then summing up the results across individual units.”

 

L’attenzione è dunque sull’eterogeneità individuale e le conseguenze distributive delle politiche.

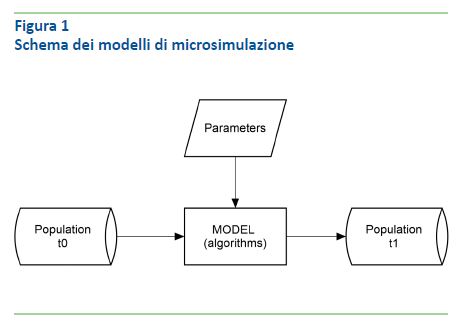
Un modello di microsimulazione è composto essenzialmente da un campione rappresentativo della popolazione di interesse e da regole che determinano cambiamenti nelle caratteristiche individuali. Queste ultime possono essere dettati istituzionali, ad esempio il funzionamento del sistema fiscale o del sistema pensionistico, oppure regolarità comportamentali, che vengono normalmente stimate nei dati. La figura 1 rappresenta lo schema generale di un modello di microsimulazione: una popolazione iniziale viene fatta evolvere sulla base di parametri derivanti o dalla legislazione o da stime. La popolazione al tempo t0 corrisponde tipicamente a una popolazione reale – così come descritta per esempio da una survey. La popolazione al tempo t1 è invece “artificiale”, nel senso che le sue caratteristiche sono simulate. Ogni corrispondenza tra le unità del campione e le unità reali diventa dunque puramente virtuale: se all’identificativo 101 corrispondeva nella popolazione di partenza il sig. Mario Rossi (non necessariamente identificato con nome e cognome) con le sue caratteristiche familiari, lavorative, reddituali ecc. così come registrate nei dati, al tempo t1 l’identificativo 101 corrisponde a un Mario Rossi virtuale, le cui caratteristiche sono potenzialmente diverse da quelle del Mario Rossi reale sia al tempo t0 (osservate), che al tempo t1 (potenzialmente ignote).

2. Modelli tax-benefit

Una classe importante di modelli di microsimulazione è composta dai modelli tax-benefit. Questi modelli ricostruiscono in maniera deterministica i benefici e gli oneri fiscali sulla base delle specifiche caratteristiche individuali e famigliari. In maniera molto semplificata, si può immaginare un modello di microsimulazione tax-benefit come un foglio di calcolo tipo Microsoft Excel, in cui le righe corrispondono a diversi individui, mentre le colonne corrispondono a diverse variabili (ad esempio, numero di figli e reddito lordo). Il modello di microsimulazione aggiunge semplicemente delle colonne contenenti ulteriori variabili, come il reddito netto disponibile. Queste variabili a volte sono direttamente osservabili nei dati di partenza, così che ci si trova con due valori per la stessa variabile: uno osservato e uno simulato. Quando questo accade è una fortuna perché consente di validare l’algoritmo (le “regole”) che ha generato il dato simulato (Sutherland 2018)^[1]. Ma perché simulare una variabile quando essa può essere osservata? Una prima risposta è che molte volte queste variabili non sono osservate. Ad esempio, molte survey riportano il reddito lordo (pre-tax) o il reddito netto (post-tax) individuale, ma non il reddito disponibile famigliare, che include anche benefici sottoposti o meno a prova dei mezzi (means tested). Inoltre, anche qualora le variabili di interesse siano osservate, la codificazione delle regole che generano il dato simulato consente di modificare qualche caratteristica individuale o qualche parametro istituzionale, e vedere quali sono gli effetti: ad esempio qual è il reddito individuale netto corrispondente allo stesso reddito lordo, in presenza di diversi scenari relativi alle aliquote contributive. Questo secondo utilizzo è a tutti gli effetti una ricostruzione controfattuale.

I modelli tax-benefit sono anche detti “statici”, perché le caratteristiche della popolazione vengono tipicamente tenute fisse. Per questo motivo, nella loro versione più semplice si limitano a identificare l’effetto diretto, “del giorno dopo”: una persona va a dormire, nel frattempo cambiano le regole del sistema fiscale, e per il semplice effetto di questo cambiamento il mattino dopo quella persona si trova più ricca, o più povera. Le sue caratteristiche non sono cambiate, così come non sono cambiati i suoi comportamenti. Se questo sembra molto semplice – addirittura semplicistico – si deve però osservare che le regole di interesse sono di solito molto complicate. Per esempio, il sistema fiscale tiene conto della posizione reddituale e patrimoniale di tutti i membri della famiglia. Per questo motivo, un semplice foglio di MS Excel di solito non basta. Inoltre, molto spesso alcune caratteristiche rilevanti non sono registrate nei dati – per esempio, il dettaglio occupazionale disponibile potrebbe essere troppo aggregato per consentire una precisa applicazione delle regole. In questo caso, il modello può funzionare solo sulla base di ipotesi semplificatrici.

I modelli di microsimulazione tax-benefit differiscono dai calcolatori fiscali. Questi ultimi sono molto diffusi e di solito consentono il calcolo delle variabili di interesse per un numero limitato di “tipi” – ad esempio una famiglia composta da due adulti e due bambini, in cui uno solo dei due adulti lavora, percependo un salario pari al salario medio. L’OCSE ha un tax-benefit calculator che discrimina solamente sulla base delle seguenti variabili:

 

• tipo famigliare (singolo o coppia);
• numero di bambini (nessuno o due);
• reddito lordo del primo componente (tra il 50% e il 200% del reddito medio, con incrementi discreti corrispondenti ad 1 punto percentuale);
• reddito lordo del secondo componente, se presente (100% del salario medio, oppure 167% del salario medio).

 

Sulla base di queste caratteristiche l’OCSE calcola, per tutti i Paesi aderenti e per un ampio numero di anni, le seguenti variabili^[2]:

 

• reddito complessivo famigliare;
• benefici legati alla casa (sulla base dell’ipotesi addizionale che la spesa per la casa sia pari al 20% del reddito medio);
• assegni famigliari;
• assistenza sociale;
• in-work benefits (indennità legate al lavoro);
• tasse sul reddito;
• contributi sociali (sulla base di ipotesi sul tipo di contratto, settore, ecc.);
• eventuale sussidio di disoccupazione (ipotizzando che la persona ne possieda i requisiti).

 

Rispetto a un simile tax-benefit calculator, un modello di microsimulazione è caratterizzato da:

 

• calcolo dettagliato della posizione fiscale sulla base di variabili individuali, per tutti gli individui nella popolazione iniziale;
• possibilità di modificare le regole e identificare chi guadagna e chi perde.

 

Con un modello di microsimulazione tax-benefit si può quindi calcolare quale sarebbe il livello di diseguaglianza, così come misurato per esempio dal coefficiente di Gini, in presenza di diversi scenari fiscali, cosa impossibile con un semplice calcolatore tax-benefit.

In Europa esistono numerosi modelli di microsimulazione tax-benefit, spesso utilizzati all’interno dei Ministeri per le analisi di bilancio e la programmazione economica, o da think tank e istituti specializzati nell’analisi delle politiche (come l’Institute for Fiscal Studies in Inghilterra). Tutti questi modelli sono però country specific, ovvero costruiti avendo una specifica realtà nazionale in mente. L’unica eccezione è EUROMOD (Sutherland e Figari 2015), che adotta le stesse scelte modellistiche per tutti i 28 Paesi dell’Unione europea^[3]. Questo consente non solo di fare confronti tra Paesi sulla base di definizioni e ipotesi comuni, ma anche di analizzare scenari controfattuali in cui regole di un Paese vengono applicate a un altro Paese.

 

3. Reazioni comportamentali

Abbiamo finora visto che anche i semplici modelli di microsimulazione tax-benefit, in cui popolazione e comportamenti vengono tenuti costanti, non sono poi così semplici, richiedendo dati, ipotesi e validazione dei risultati. Modelli di microsimulazione più sofisticati tengono conto di reazioni comportamentali (behavioural). In altri termini, se cambiano gli incentivi, è lecito attendersi che cambino anche i comportamenti individuali. Per esempio, se aumentano le aliquote marginali, gli individui possono reagire sia lavorando di più, per compensare il minore reddito netto associato a ciascuna ora di lavoro, sia lavorando di meno, dal momento che lo stesso sacrificio di rinuncia al tempo libero è associato a una minore contropartita monetaria (il costo-opportunità del tempo libero diminuisce, quindi le persone ne vogliono “consumare” di più). Il primo effetto è chiamato effetto di reddito, mentre il secondo è chiamato effetto di sostituzione. Un risultato standard nella letteratura sull’offerta di lavoro è che normalmente l’effetto di sostituzione prevale sull’effetto di reddito (Bargain et al. 2014). Questo significa che un aumento delle tasse risulta in un aumento del gettito minore di quanto atteso in un modello puramente aritmetico, non comportamentale: il cambiamento nei comportamenti riduce l’effetto della politica. Introdurre effetti comportamentali significa introdurre nuove equazioni nel modello che determinano come cambiano le circostanze individuali. Indichiamo con Y le variabili di outcome (ad esempio, il reddito disponibile), con X le scelte individuali (ad esempio, il numero di ore lavorate), con W il salario, con Z le altre caratteristiche individuali (ad esempio, istruzione e composizione famigliare) e con P i parametri di policy (il sistema fiscale):

 

(1)Y_t=f(X_t, W_t, Z_t, P_t)

 

dove f è una mappa potenzialmente multidimensionale. Tutte le variabili ad eccezione di quelle di policy (“la legge è eguale per tutti”) sono definite a livello individuale, ma per comodità di notazione tralasciamo gli identificativi individuali.

Un modello puramente aritmetico tiene fissi X, W e Z, e considera solamente cambiamenti nelle politiche P. Reazioni comportamentali implicano cambiamenti in alcune delle variabili X, che vanno modellati come processi a sé stanti:

 

(2)X_t=g(W_t, Z_t, P_t).

 

Nel nostro esempio, il numero di ore lavorate potrebbe essere stimato nei dati sulla base del salario potenziale W e delle caratteristiche individuali Z, mentre gli incentivi del sistema fiscale potrebbero essere catturati da una serie di parametri, come struttura delle aliquote, ecc. La stima di un simile modello è però possibile solamente se nei dati vi è sufficiente variabilità in tutte le variabili, incluse quelle di policy. Un’alternativa è quella di adottare un modello strutturale, in cui per esempio gli individui scelgono la quantità di lavoro offerta cercando di massimizzare l’utilità individuale o famigliare (Aaberge e Colombino 2018). Per semplicità si considera di solito un numero limitato di opzioni (modelli a scelta discreta): ad esempio 0, 10, 20, 30, 40, o 50 ore di lavoro alla settimana (la scelta delle opzioni viene guidata dalla distribuzione delle ore lavorate osservate nei dati). Se il modello considera che la scelta avvenga in modo congiunto a livello famigliare (modello cosiddetto unitario), abbiamo quindi un massimo di 5 alternative per le famiglie con un solo adulto (con o senza figli), e di 25 per le famiglie in cui sono presenti due partner (di nuovo, con o senza figli)^[4]. Per ognuna di queste scelte si applica il modello di simulazione tax-benefit per ottenere – sulla base della struttura dei salari stimata nei dati – un valore di reddito disponibile famigliare, tenendo conto di tasse e benefici. Quindi si stimano i parametri “strutturali” delle funzioni di utilità individuali che pesano opportunamente reddito disponibile e tempo libero, tenendo conto di un elemento idiosincratico (RUM: Random Utility Models). Un cambiamento nei parametri del sistema fiscale implica un cambiamento nel reddito disponibile associato alle diverse scelte e quindi – ipotizzando che le preferenze individuali non cambino – un possibile cambiamento nelle scelte lavorative. Si noti che la massimizzazione dell’utilità è uniperiodale, ovvero relativa solamente al periodo corrente. Modelli più complicati considerano anche gli effetti delle scelte X sull’utilità futura (comportamento forward looking)^[5]. Se un semplice modello tax-benefit permette di analizzare gli effetti del giorno dopo delle politiche, un modello con reazioni comportamentali, che mantiene le caratteristiche individuali costanti ma permette agli individui di aggiustare le proprie scelte per tenere conto del cambiamento negli incentivi, permette di analizzare gli effetti nel breve-medio periodo (qualche mese).

I modelli di offerta di lavoro ora esaminati richiedono di calcolare quello che sarebbe il reddito lordo – e quindi, dopo l’applicazione del modello tax-benefit, il reddito disponibile – anche per gli individui che vengono osservati non lavorare. Ciò richiede la stima di un’equazione dei salari, che assegni un salario orario potenziale W ad ogni individuo nella popolazione sulla base delle sue caratteristiche osservate (come livello di istruzione ecc.), a prescindere dallo stato lavorativo. Questo salario orario viene mantenuto constante in tutte le scelte, e in tutti gli scenari relativi alle politiche. Oltre alle altre caratteristiche individuali Z, in un modello statico, vengono tenute costanti: età, istruzione, composizione famigliare, stato di salute ecc.

4. Modelli dinamici

Passando a una popolazione dinamica, con un orizzonte temporale più ampio, l’ipotesi che queste variabili rimangano costanti non può ovviamente essere più sostenuta. L’età cambia, in modo deterministico. Ma anche il livello di istruzione cambia, e in modo non deterministico, così come cambia la composizione famigliare, lo stato di salute ecc. Inoltre, queste variabili vanno inizializzate per tutti i “nuovi nati” nella simulazione. Un modo per modellare questi cambiamenti è adottare un semplice modello markoviano, in cui le caratteristiche al tempo t vengono fatte dipendere dalle caratteristiche al tempo t-1:

 

3) Z_t=h(Y_t-1, X _t-1, Z _t-1, W _t, P _t)

 

I valori iniziali Z₀ vengono tipicamente estratti da una distribuzione, che può essere mantenuta costante nei diversi periodi della simulazione, oppure subire modifiche sulla base di trend individuati nei dati osservati.

Se un modello statico permette di analizzare la distribuzione di Y rispetto alle caratteristiche Z della popolazione, un modello dinamico permette anche di fare previsioni su come cambieranno queste caratteristiche nel tempo (Li e O’Donogue 2014). Ad esempio, in un recente lavoro (Richardson et al. 2018) abbiamo sviluppato un modello di microsimulazione dinamico per fare previsioni di lungo periodo sull’evoluzione dei tassi di partecipazione in sei Paesi europei (cinque Paesi a bassa partecipazione: Italia, Spagna, Irlanda, Ungheria e Grecia, e un Paese ad alta partecipazione utilizzato come benchmark, la Svezia), con un focus particolare su partecipazione femminile. Il modello considera i seguenti processi (moduli): (i) invecchiamento, (ii) scelte scolastiche, (iii) formazione e dissoluzione delle famiglie, (iv) maternità, (v) scelta di partecipazione al mercato del lavoro^[6]. Il vantaggio di utilizzare un modello di microsimulazione, rispetto per esempio ad un modello più aggregato come quello della Commissione europea (European Commission 2014), è triplice:

 

• Il modello di microsimulazione, generando un panel di dati simulati, consente di analizzare i risultati a qualunque livello di aggregazione – per esempio calcolando ex-post il tasso di partecipazione per le donne tra i 25 e 40 anni con un figlio di età inferiore ai 3 anni. Modelli più aggregati richiedono la definizione degli aggregati di interesse ex-ante, e spesso limitano la scelta di questi stessi aggregati.
• Il modello di microsimulazione consente un’analisi dell’incertezza intorno alle proiezioni assente nei modelli aggregati, che devono ricorrere a scenari arbitrari sull’evoluzione delle caratteristiche della popolazione. Nella microsimulazione, al contrario, l’evoluzione delle caratteristiche della popolazione viene stimata nei dati. Considerando l’effetto congiunto dell’incertezza nella stima di ciascun parametro per ciascuno dei moduli della microsimulazione si possono ottenere intervalli di confidenza intorno alle proiezioni.
• Il modello di microsimulazione produce previsioni non solamente rispetto all’output di interesse, ma anche rispetto all’evoluzione delle sue determinanti.

5. Effetti di equilibrio generale

Un ulteriore livello di complicazione è rappresentato dalla considerazione che la struttura dei salari non può rimanere invariata se cambia l’offerta di lavoro, soprattutto in un’ottica di medio o lungo periodo. Ad esempio, se immaginiamo che i salari siano determinati dall’incontro tra domanda e offerta di lavoro, a un aumento dell’offerta di lavoro deve corrispondere una diminuzione dei salari. In questo modo l’iniziale eccesso di offerta viene riassorbito, perché la riduzione dei salari scoraggia l’offerta riducendo l’iniziale aumento, e al tempo stesso incoraggia la domanda di lavoro da parte delle imprese. In altri termini, nel nostro semplice schema alcune delle variabili Z sono anch’esse endogene. Un modo per tenere conto di questi effetti di equilibrio generale nel mercato del lavoro è fare interagire il modello di microsimulazione dell’offerta di lavoro con un modello della domanda di lavoro, eventualmente mantenuto a un livello più aggregato (per esempio, distinguendo per livelli di istruzione). Altri modelli considerano anche l’evoluzione endogena delle principali variabili macroeconomiche, dai prezzi al valore aggiunto^[7]. Un approccio utilizzato in letteratura (Peichl e Siegloch 2012) prevede di stimare l’elasticità della domanda di lavoro al salario (distinguendo tra elasticità dirette e incrociate per livelli di istruzione). Il salario viene quindi aggiustato in modo da equilibrare la nuova offerta di lavoro, così come determinata dal modello di microsimulazione, con la domanda di lavoro. In un’ottica di medio o lungo periodo anche il livello della domanda di lavoro deve essere in grado di modificarsi endogenamente, per esempio per effetto della crescita della popolazione e del cambiamento tecnologico.

Una rappresentazione schematica è fornita in figura 2.

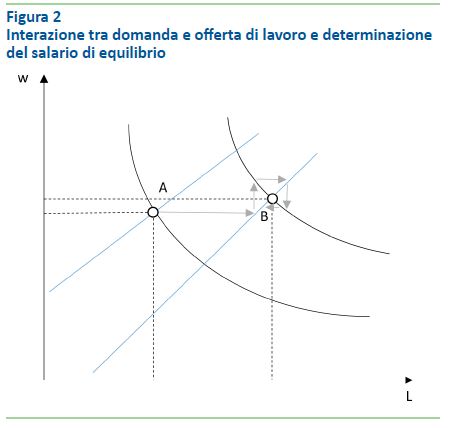
La curva decrescente passante per A – l’equilibrio iniziale – rappresenta la domanda di lavoro nel periodo iniziale, di cui viene stimata l’elasticità. La retta crescente passante per il punto A è l’offerta di lavoro, in corrispondenza di determinate politiche P. Essa è determinata dal modello di microsimulazione. Al cambiamento delle politiche, l’offerta di lavoro si sposta verso destra (retta crescente passante per il punto B). A salari costanti, questo determinerebbe un eccesso di offerta di lavoro. Ma anche la curva di domanda di lavoro si sposta verso destra (curva decrescente passante per B), determinando un aggiustamento dei salari di equilibrio. Se le elasticità dell’offerta e della domanda di lavoro rispettano certe condizioni, il sistema si comporta come un modello della ragnatela (cobweb model) e il nuovo equilibrio in B è raggiungibile e stabile. Si noti che nel breve periodo (quindi prima che la curva di domanda di lavoro si sposti verso destra) la considerazione degli effetti di retroazione via domanda di lavoro agisce in maniera opposta agli effetti comportamentali via offerta di lavoro, riavvicinando il modello ai risultati del modello tax-benefit originario. Un aumento delle tasse, ad esempio, causa nel breve periodo una riduzione dell’offerta di lavoro, con conseguente riduzione del gettito, ma anche un aumento dei salari, con un effetto positivo sul gettito. Nel medio-lungo periodo questo effetto di aumento dei salari può essere a sua volta compensato dall’aumento della domanda di lavoro, potenzialmente innescato dallo stesso aumento dei salari (i salari sono parte della domanda aggregata).

Questo meccanismo di interazione tra domanda e offerta di lavoro nel lungo periodo è utilizzato nel modello di microsimulazione denominato LABOURsim su cui il mio gruppo di ricerca sta attualmente lavorando, che ha anche beneficiato del supporto di Inapp. Il funzionamento di questo modello è descritto in figura 3.

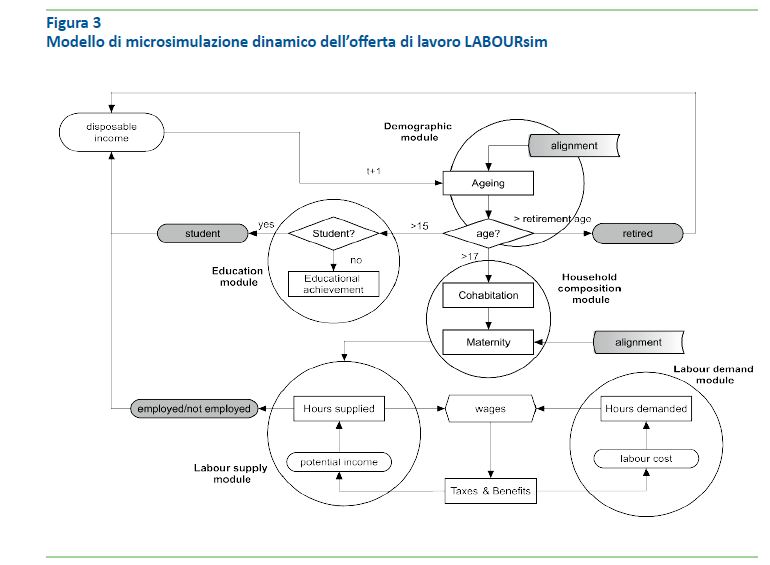
La figura 4 infine riassume i diversi livelli di sofisticazione che possono essere incorporati in un modello di microsimulazione del mercato del lavoro.

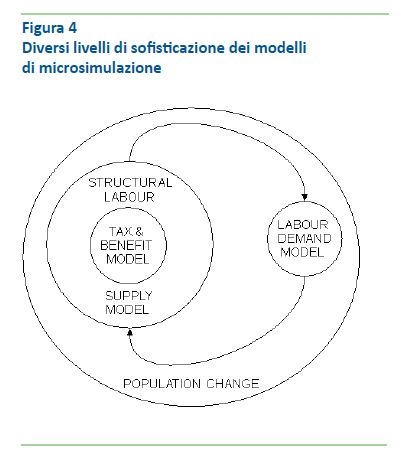
Al centro vi è il semplice modello tax-benefit, puramente aritmetico. Esso può essere incorporato in un modello strutturale dell’offerta di lavoro, così come descritto sopra.

Questo modello di offerta di lavoro può interagire con un modello di domanda di lavoro, determinando endogenamente la struttura dei salari. Tutto questo però avviene con una popolazione statica. Il modello può essere ulteriormente arricchito considerando, con un orizzonte temporale più ampio, cambiamenti nella popolazione: invecchiamento, nascite e morti, formazione e dissoluzione delle famiglie, istruzione, pensionamento ecc.

6. Conclusioni

L’approccio alla valutazione delle politiche tramite microsimulazione è estremamente flessibile, e da un certo punto di vista has history on its side. L’utilizzo crescente delle simulazioni al computer ha rivoluzionato il modo di fare scienza: dall’ingegneria alla biologia, dalla meteorologia alla matematica applicata, i modelli computazionali sono oramai onnipresenti. I modelli di simulazione tax-benefit, per quanto concettualmente semplici, sono strumenti potenti per analizzare vincitori e perdenti in conseguenza di cambiamenti reali o ipotetici nelle politiche. Il fatto che lo sviluppo di questi modelli sia estremamente laborioso, e che essi possano avere un ruolo importante nell’indirizzare le scelte politiche, aiuta forse a spiegare come mai molti di questi modelli rimangono proprietari, sviluppati internamente da agenzie governative o centri di ricerca pubblici o privati e non accessibili dall’esterno. In Europa però questa logica è superata grazie a EUROMOD, un modello tax-benefit per tutti e 28 i Paesi dell’Unione europea utilizzato, oltre che per fini di ricerca, anche per analisi pubbliche di bilancio (ad esempio da parte del Governo regionale Scozzese) e per la produzione di rapporti e statistiche da parte della Commissione europea ed Eurostat. La disponibilità di EUROMOD rende veloce ed economica l’analisi controfattuale degli effetti diretti, aritmetici, di molte politiche fiscali.

Modelli con risposte comportamentali e modelli dinamici, con orizzonti temporali più ampi, sono utili per prevedere l’effettivo impatto delle politiche su povertà e diseguaglianza, e per valutare l’effetto congiunto dei diversi trend identificabili nei dati, dall’aumento della scolarità all’aumento del numero dei divorzi, delle famiglie mono-parentali, dei contratti temporanei. Questi modelli sono però basati su ipotesi più forti, spesso sviluppate all’interno di gruppi di ricerca con fini accademici e anch’essi non disponibili all’esterno. Ciò sta tuttavia cambiando. La disponibilità di piattaforme di microsimulazione open source come JAS-mine (Richiardi e Richardson 2017) permette infatti di accelerare lo sviluppo di nuovi modelli utilizzando:

 

• librerie e soluzioni già pronte e integrate nella piattaforma – un esempio è costituito dagli algoritmi per la creazione delle famiglie, per l’allineamento dei risultati aggregati delle simulazioni rispetto a target esterni, per l’importazione di modelli econometrici;
• modelli esistenti sviluppati sulla stessa piattaforma, che possono essere modificati sulla base di convenzioni e soluzioni comuni, contribuendo a creare un’ecologia di modelli (Richiardi 2017) in cui le diverse e alternative ipotesi e scelte modellistiche possano essere confrontate e contribuire a creare standard comuni e accettati.

Bibliografia

Aaberge R., Colombino U. (2018), Structural labour supply models and microsimulation, International Journal of Microsimulation 11(1), [forthcoming]

Bargain O., Orsini K., Peichl A. (2014), Comparing Labor Supply Elasticities in Europe and the United States. New Results, Journal of Human Resources, 49, n.3, pp.723-838

European Commission (2014), The 2015 Ageing Report. Underlying Assumptions and Projection Methodologies, European Economy 8/2014 < goo.gl/wQ56vb >

Keane M.P., Wolpin K.I. (2009), Empirical applications of discrete choice dynamic programming models, Review of Economic Dynamics, 12, n.1, pp.1-22

Klevmarken N.A. (2001), Micro-simulation. A tool for economic analysis, Working Paper 2001:13, Uppsala, Uppsala University Department of Economics

Li J., O’Donoghue C. (2014), A survey of dynamic microsimulation models: uses, model structure and methodology, International Journal of Microsimulation, 6, n.2, pp.3-55

Martini A., Trivellato U. (1997), The role of survey data in microsimulation models for social policy analysis, Labour, 11, n.1, pp.83-112

Orcutt G. (1957), A new type of socio-economic system, Review of Economics and Statistics, 36, n.2, pp.116-123

Peichl A., Siegloch S. (2012), Accounting for labor demand effects in structural labor supply models, Labour Economics, 19, n.1, pp.129-138

Richardson R., Pacelli L., Poggi A., Richiardi M. (2018), Female labour force projections using microsimulation for six EU countries, International Journal of Microsimulation [forthcoming]

Richiardi M. (2017), The Future of Agent-Based Modelling, Eastern Economic Journal, 43, n.2, pp.271-287

Richiardi M., Richardson R.E. (2017), JAS-mine. A New Platform for Microsimulation and Agent-Based Modelling, International Journal of Microsimulation, 10, n.1, pp.106-134

Sutherland H., Figari F. (2015), EUROMOD: the European Union tax-benefit microsimulation model, International Journal of Microsimulation, 6, n.1, pp.4-26

Sutherland H. (2018), Quality assessment of microsimulation models: the case of EUROMOD, International Journal of Microsimulation, 11, n.1, [forthcoming]

van de Ven J. (2017), Exploring the Importance of Incentive Responses for Policy Projections, International Journal of Microsimulation, 10, n.3, pp.134-164

L’autore

Matteo Richiardi

matteo.richiardi@spi.ox.ac.uk

Professore di Economia presso l’Università di Essex, direttore di EUROMOD e Editor-in-chief dell’International Journal of Microsimulation. Fra le sue pubblicazioni recenti si segnalano Banks, firms and jobs (Review of Financial Studies, con F. Berton, S. Mocetti e A. Presbitero), Agent-based models in economics: a toolkit (Cambridge University Press, con D. Delli Gatti, M. Gallegati, G. Fagiolo e A. Russo) e Agent-based models of the labor market (Handbook of Computational Economics and Finance, Oxford University Press, con M. Neugart).

---